Metrics Notes

Table of contents

1. Metrics Notes
   1. Entropy
   2. Perplexity
   3. References

Entropy

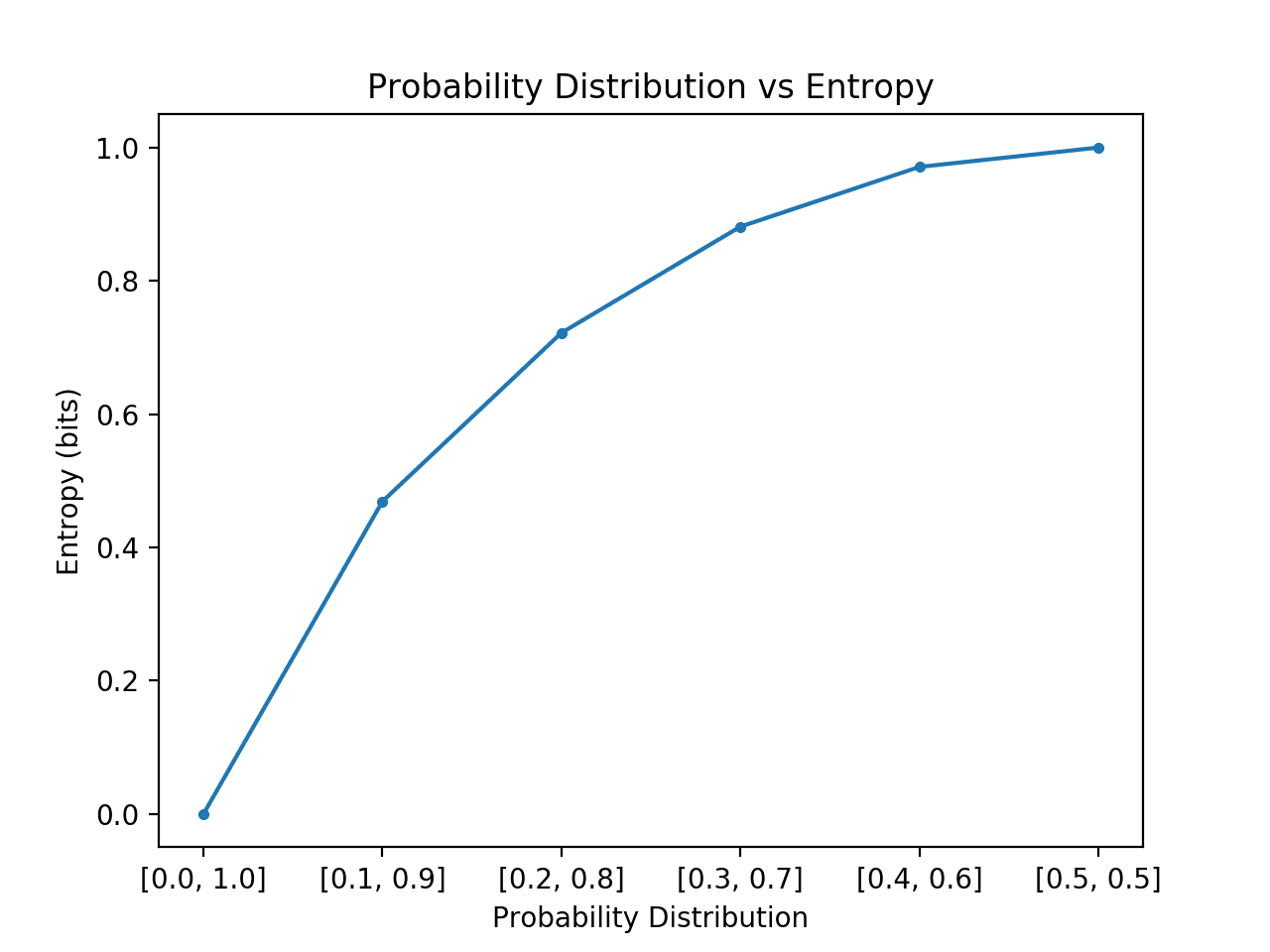
An information content or uncertainty measurements. The higher the entropy, the harder to predict value of an random variable from a given distribution.

The entropy of a discrete random variable $X$ with distribution $p$ consisting of $K$ states is:

$\begin{aligned} H(X) &\triangleq -\sum^K_{k=1}{p(X=k)}\\ &=-\mathbb{E}_X[\log{p(X)}] \end{aligned}$

Intuitions

For example, let $X_n$ be a random variable from distribution $p$: $X_n\sim p$ over $K$ states.

If we have three random variables $X^1_n, X^2_n, X^3_n$ from three corresponding dist. $p^1,p^2,p^3$.

Intuitively speaking, according to the given information, the prediction of $X^1$ and $X^2$ should be with higher confidence than $X^3$:

• In $X^1$ case: we could somewhat predict that $k_1$ should likely to be observed. Likewise, it’s $k_0$ for $X^2$
• However, for $X^3$ it’s impossible for any prediction (50:50).

Is there anyway to define a measurement to how “confident” our prediction would be with given information about $K$ states? By dividing and conquer this question, the sub question should be:

How to measure the prediction’s confidence for a given state $K_i$

• $X$ is said to have low entropy, or rich amount of information; if using $X$ we could easily predict a specific event of $P(X=k_i)$

Perplexity

To measure “predictability”. Given $p$ is a uniform dist. over $K$ state

References

1. Murphy, K. P. (2022). Probabilistic Machine Learning: An introduction. MIT Press. probml.ai
   LINK