Skip to main content Link Menu Expand (external link) Document Search Copy Copied
Nguyen'Log
Table of contents
  1. Overview
  2. Notation
  3. Vector
  4. References

Overview

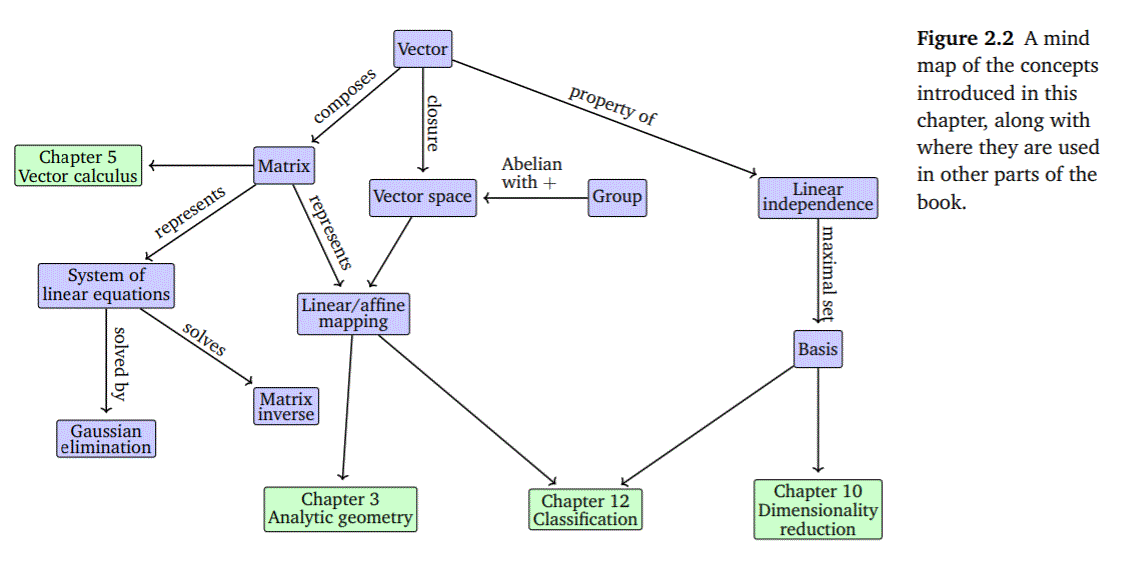Figure 1 Figure 1: Linear Algebra mindmap (Deisenroth et al., 2020)

Notation

Name Description Example LaTeX
Vector Bold, lowercase font x=[x1x2⋮xm],x∈Rn\boldsymbol{x}=\begin{bmatrix} x_{1} \\ x_{2} \\ \vdots \\ x_{m}\end{bmatrix}, \boldsymbol{x}\in \mathbb{R}^n $ \boldsymbol{x} $
Matrix Bold, uppercase font A=[a1,1…a1,m⋮⋱⋮an,1…an,m]\boldsymbol{A}=\begin{bmatrix} a_{1,1} & \dots & a_{1,m} \\ \vdots & \ddots & \vdots \\ a_{n,1} & \dots & a_{n,m} \end{bmatrix},
A∈Rn×m\boldsymbol{A}\in \mathbb{R}^{n\times m}		 $ \boldsymbol{A} $
Matrix Entry   Ai,j\boldsymbol{A}_{i,j} is the entry in the
ithi^{th} row and jthj^{th} column		 $ \boldsymbol{A}_{i,j} $
Matrix Row iith row of A\boldsymbol{A} is denoted as aiTa_i^T or Ai,:A_{i,:} A=[—a1T—⋮—anT—]\begin{aligned}\boldsymbol{A}=\begin{bmatrix}\text{---} & a_1^T & \text{---} \\ & \vdots & \\ \text{---} & a_n^T & \text{---}\end{bmatrix}\end{aligned}  
Matrix Column jjth column of AA is denoted as aja_j or A:,jA_{:,j} A=[∣∣∣a1…an∣∣∣]\begin{aligned}\boldsymbol{A}=\begin{bmatrix} \mid & \mid & \mid \\ a_1 & \dots & a_n \\ \mid & \mid & \mid \end{bmatrix}\end{aligned}  

Vector

References

  1. Deisenroth, M. P., Faisal, A. A., & Ong, C. S. (2020). Mathematics for Machine Learning. Cambridge University Press. https://doi.org/10.1017/9781108679930
  2. Mathematical objects. (2021). https://dynref.engr.illinois.edu/rvn.html
    [Online; accessed 2021-07-18]
  3. Petulla, S. (2021). Linear algebra cheatsheet. https://observablehq.com/@petulla/explorable-linear-algebra-cheatsheet
    [Online; accessed 2021-08-13]
  4. Kolter, Z., & Do, C. (2015). Linear Algebra Review and Reference. http://cs229.stanford.edu/section/cs229-linalg.pdf
    [Online; accessed 2021-08-13]
  5. Computational Linear Algebra for Coders. (2021). https://github.com/fastai/numerical-linear-algebra
    [Online; accessed 2021-08-13]
  6. Linear Algebra for Deep Learning. (2021). https://www.quantstart.com/articles/scalars-vectors-matrices-and-tensors-linear-algebra-for-deep-learning-part-1/
    [Online; accessed 2021-08-13]
  7. Immersive Linear Algebra. (2021). http://immersivemath.com/ila
    [Online; accessed 2021-08-13]
  8. Strang, G. (2009). Introduction to Linear Algebra (Fourth). Wellesley-Cambridge Press.