Derivatives

Table of contents

Derivatives
References

Objectives

Derivatives

Definition

Interpretation

Derivatives

Differentiation is a process of taking derivative.

The derivative of $f(x)$ with respect to x is the function $f^\prime(x)$ :

$f^\prime(x) = \lim_{h\to 0}{\frac{f(x+h) - f(x)}{h}}$ $(f^\prime \quad \text{called} \quad f \quad \text{prime of} \quad x)$

View more about the origin of the term

Origin of Differentiation terminologies

The following information are just opinions originated by Math SE, Quora, and Wikipedia:

Derivative implies a derived function $f^\prime(x)$ of the original $f(x)$ , the final product which is obtained from the Differentiation of the same function.

Differentiate could refers to the the word ‘difference’ as Leibniz studied finite differences and introduce (infinitesimal) differentials.

Differential means a mathematical expression using differentials (e.g. $\mathrm{d}y, \mathrm{d}x,\frac{\mathrm{d}y}{\mathrm{d}x}$ )

There are 2 major interpretations for a derivative of a function:

Rate of change
Slope of tangent line

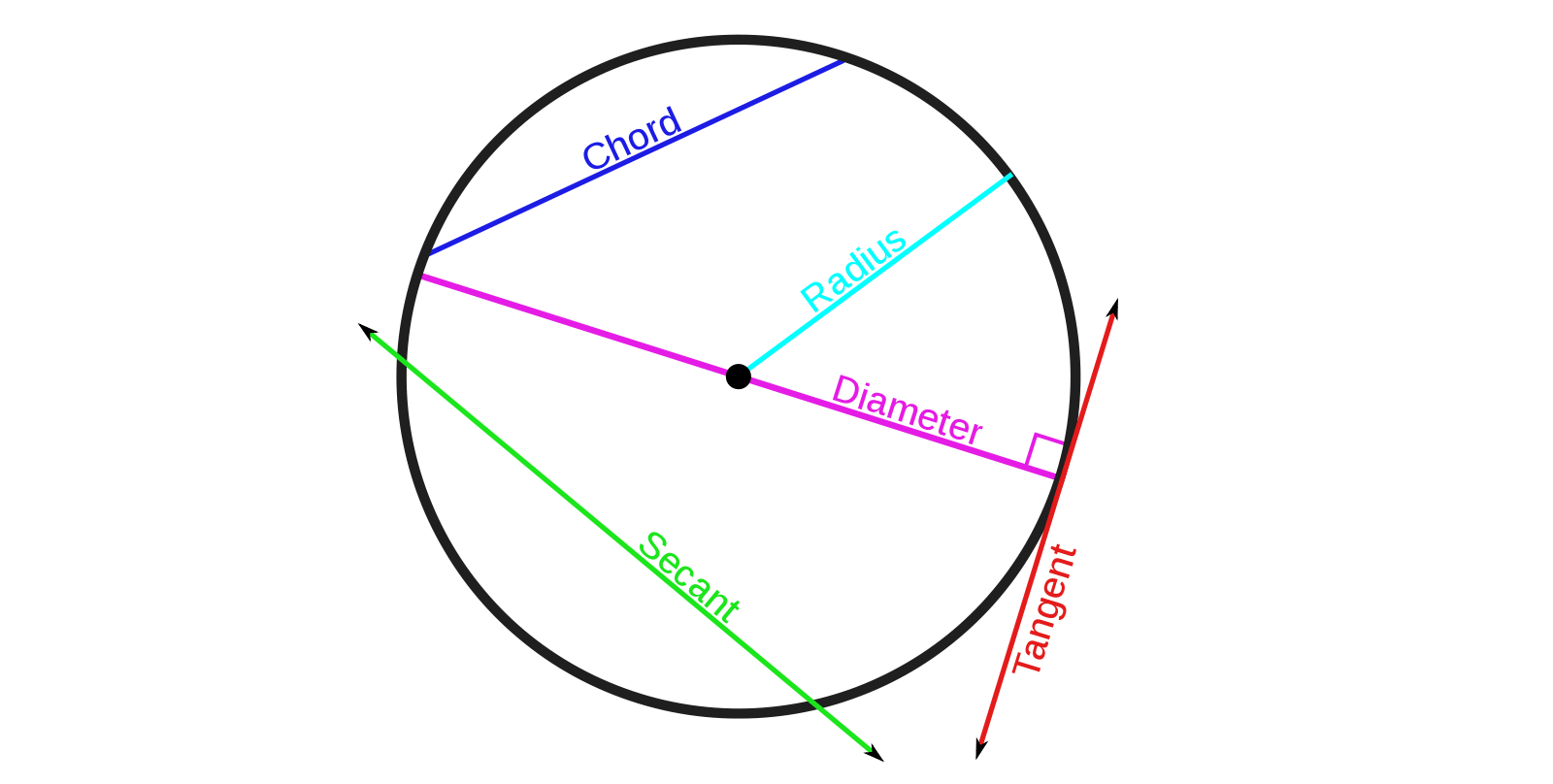line_kinds Figure 1: Common lines and line segments on a circle (Wikipedia: Secant Line, 2021)

To understand a tangent line, the secant line concept has to come first.

A secant is a line that intersects a curve at a minimum of two distinct points.

(Wikipedia: Secant Line, 2021)

Then,

A tangent line is a line that intersects a curve at two infinitely close points

― Gottfried Wilhelm Leibniz

If we draw a secant line at $\left(a, f(a)\right)$ , the slope of this line is: $m_{sec} = Q = \frac{f(x) - f(a)}{x - a}$

This equation forms a difference quotient. Suppose $\forall h\ne 0: x = a + h$ , the aforementioned equation can also be expressed as: $Q = \frac{f(a + h) - f(a)}{h}$

Also, from the above properties, one could infer the slope $m_{tangent}$ of the tangent line of $f(x)$ at $x=a$ is:

$\begin{aligned} m_{tangent} = f^\prime(a) &= \lim_{x\to a}{\frac{f(x) - f(a)}{x - a}} \\ &= \lim_{\Delta{x}\to 0}{\frac{\Delta{f(x)}}{\Delta{x}}} \end{aligned}$

To summary,

$\begin{aligned} \text{Secant line} &= \frac{\Delta{f(x)}}{\Delta{x}} & &= \text{Average rate of change} \\ \text{Tangent line} &= \lim_{\Delta{x}\to 0}{\frac{\Delta{f(x)}}{\Delta{x}}} & &= \text{Instantaneous rate of change} \end{aligned}$

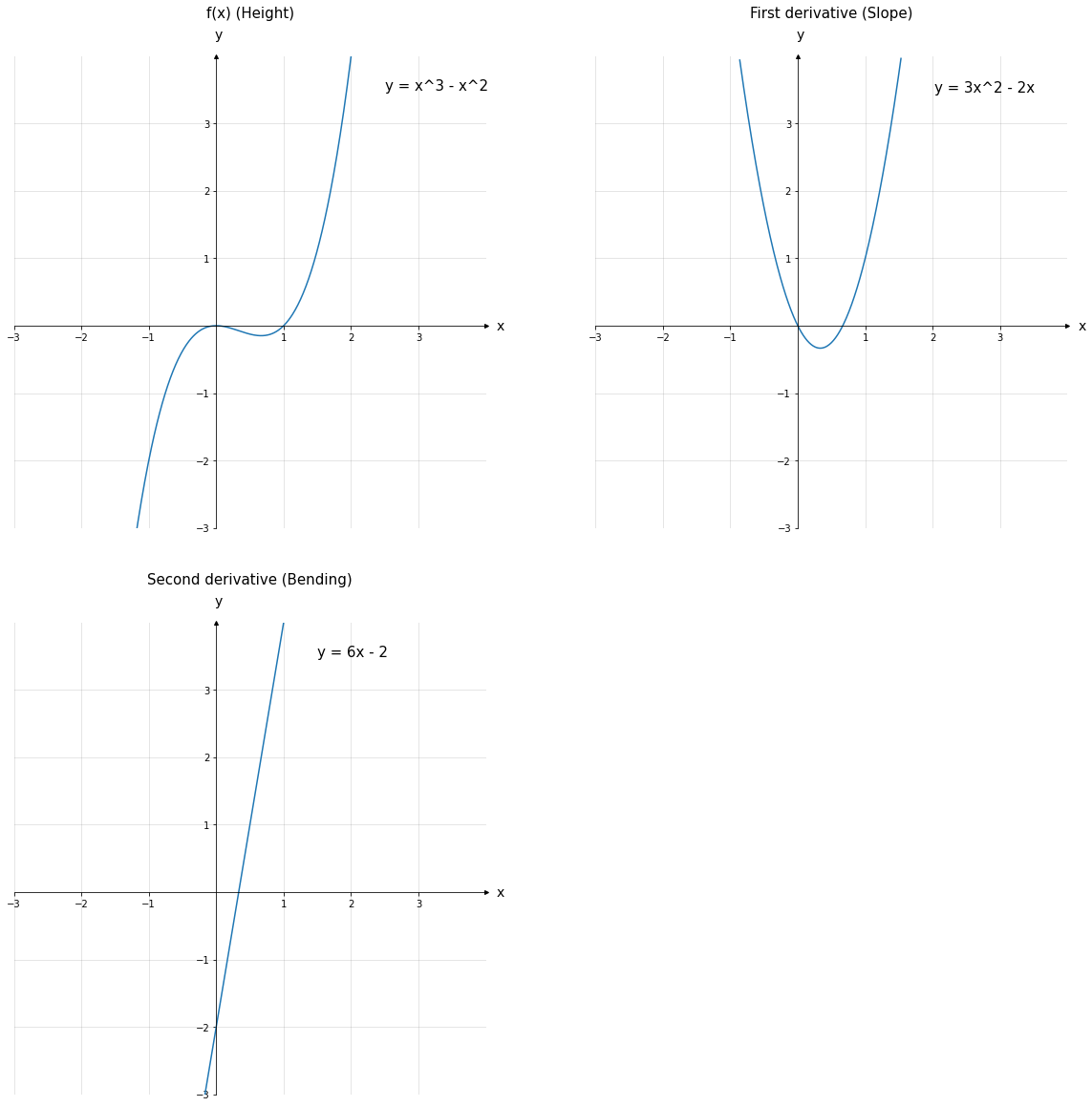png Figure 2: Examples of derivatives

Code for Fig. 2

import warnings
warnings.filterwarnings('ignore')
import logging
logging.basicConfig(
    format='%(asctime)s %(levelname)-8s %(message)s',
    level=logging.INFO,
    datefmt='%Y-%m-%d %H:%M:%S')

import tensorflow as tf
from matplotlib import pyplot as plt

import numpy as np

class CartesCoordinator:
  """
    Collection of utils for vector operation samples and exercise
  """
  def draw_coord(ax, xlim=(-5,5), ylim=(-5,5), tick_freq=1, aspect=1):
    xmin, xmax = xlim
    ymin, ymax = ylim

    ax.set(xlim=(xmin, xmax + tick_freq), ylim=(ymin, ymax + tick_freq), aspect=aspect)

    # Employ bottom, left spines as x,y axes
    ax.spines['bottom'].set_position('zero')
    ax.spines['left'].set_position('zero')

    # Remove top, right spines
    ax.spines['top'].set_visible(False)
    ax.spines['right'].set_visible(False)

    # Set x,y label on axes
    ax.set_xlabel('x', size=14, labelpad=-24, x=1.03)
    ax.set_ylabel('y', size=14, labelpad=-24, y=1.03, rotation=0)

    x_ticks = np.arange(xmin, xmax+tick_freq, tick_freq)
    y_ticks = np.arange(ymin, ymax+tick_freq, tick_freq)

    # Draw major and minor grid lines
    ax.grid(which='both', color='grey', linewidth=1, linestyle='-', alpha=0.2)

    ax.set_xticks(x_ticks[x_ticks != 0])
    ax.set_yticks(y_ticks[y_ticks != 0])

    # Arrows for axes
    arrow_fmt = dict(markersize=4, color='black', clip_on=False)
    ax.plot(1, 0, marker='>', transform=ax.get_yaxis_transform(),**arrow_fmt)
    ax.plot(0, 1, marker='^', transform=ax.get_xaxis_transform(),**arrow_fmt)

class DerivativeVisualization:
  def draw_f(ax, f, func_name, x_lim, y_lim, delta=0.01, X_in=None, alpha=1, tick_freq=1):
    X = X_in if (X_in is not None) else tf.range(x_lim[0] - delta, x_lim[1] + delta, delta=delta)

    X = tf.boolean_mask(X, tf.less(f(X), y_lim[1] + tick_freq))
    Y = f(X)

    # Draw f(x)
    ax.plot(X, Y, '-', alpha=alpha)
    ax.text(X[-1] + 0.5, Y[-1] - 0.5, func_name, fontsize=15)

from matplotlib import ticker

tf.random.set_seed(32)

x_domain = (-3, 3)
y_domain = (-3, 3)
fig, ax = plt.subplots(2, 2,figsize=(20,20))

### f(x)
f = lambda x: (x**3 - x**2)

ax[0,0].set_title('f(x) (Height)', pad=40, size=15)
CartesCoordinator.draw_coord(ax[0,0], x_domain, y_domain, aspect=1)
DerivativeVisualization.draw_f(ax[0,0], f, 'y = x^3 - x^2', x_domain, y_domain)

### f'(x)
f = lambda x: (3*x**2 - 2*x)

ax[0,1].set_title('First derivative (Slope)', pad=40, size=15)
CartesCoordinator.draw_coord(ax[0,1], x_domain, y_domain, aspect=1)
DerivativeVisualization.draw_f(ax[0,1], f, 'y = 3x^2 - 2x', x_domain, y_domain)

### f''(x)
f = lambda x: (6*x - 2)

ax[1,0].set_title('Second derivative (Bending)', pad=40, size=15)
CartesCoordinator.draw_coord(ax[1,0], x_domain, y_domain, aspect=1)
DerivativeVisualization.draw_f(ax[1,0], f, 'y = 6x - 2', x_domain, y_domain)

fig.delaxes(ax[1,1])

plt.show()

References

Wikipedia: Secant line. (2021). https://en.wikipedia.org/wiki/Secant_line
[Online; accessed 2021-07-28]

LINK