Skip to main content Link Menu Expand (external link) Document Search Copy Copied
Nguyen'Log

Differentiation Formulas

Table of contents
  1. Differentiation Formulas
    1. Trig Functions
    2. Exponential functions
      1. Number e
    3. Inverse of Trig functions
      1. Inverse Sine
      2. Summary: Inverse trig functions
    4. References

Objectives

Differentiation Formulas

  • Trig functions
  • Exponential functions
  • Logarithm functions
  • Hyperbolic functions

Trig Functions

WIP

Below are popular six trig functions:

cos⁡xsin⁡xtan⁡x=sin⁡xcos⁡xcot⁡x=cos⁡xsin⁡xsec⁡x=1cos⁡xcsc⁡x=1sin⁡x \begin{aligned} \cos{x} & \quad&& \sin{x}& \\ \tan{x} &=\frac{\sin{x}}{\cos{x}} \quad&& \cot{x}&=\frac{\cos{x}}{\sin{x}} \\ \sec{x} &=\frac{1}{\cos{x}} \quad&& \csc{x}&=\frac{1}{\sin{x}} \end{aligned}

More reviews could be found here

trig_functions

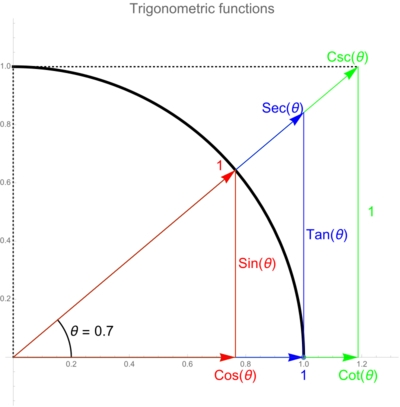
Figure 3: Trigonometric functions (Wikipedia: Trigonometric Functions, 2021)

  Function ff Derivative f′f^\prime
sin f(x)=sin(x)f(x) = sin(x) f′(x)=cos(x)f^\prime(x)=cos(x)
cos f(x)=cos(x)f(x) = cos(x) f′(x)=−sin(x)f^\prime(x)=-sin(x)
tan f(x)=tan(x)f(x) = tan(x) f′(x)=1cos2(x)=sec2(x)f^\prime(x)=\frac{1}{cos^2(x)}=sec^2(x)
cot f(x)=cot(x)f(x) = cot(x) f′(x)=−1sin2(x)=−csc2(x)f^\prime(x)=-\frac{1}{sin^2(x)}=-csc^2(x)

Exponential functions

Number e

WIP

The number ee is an important mathematical constant, approximately equal to 2.71828...2.71828....

Three general definitions of ee are:

  • e=lim⁡n→∞(1+1n)ne = \lim_{n\to \infin}{(1+\frac{1}{n})^n}
  • lim⁡h→0eh−1h=1\lim_{h\to 0}{\frac{e^h-1}{h}} = 1
  • e=∑n=0∞1n!e = \sum_{n=0}^{\infin}{\frac{1}{n!}}

Eucler’s Number: Intuitions

Code for Fig. 2 
import warnings
warnings.filterwarnings('ignore')
import logging
logging.basicConfig(
    format='%(asctime)s %(levelname)-8s %(message)s',
    level=logging.INFO,
    datefmt='%Y-%m-%d %H:%M:%S')

import tensorflow as tf
from matplotlib import pyplot as plt

import numpy as np

class CartesCoordinator:
  """
    Collection of utils for vector operation samples and exercise
  """
  def draw_coord(ax, xlim=(-5,5), ylim=(-5,5), tick_freq=1, aspect=1):
    xmin, xmax = xlim
    ymin, ymax = ylim

    ax.set(xlim=(xmin, xmax + tick_freq), ylim=(ymin, ymax + tick_freq), aspect=aspect)

    # Employ bottom, left spines as x,y axes
    ax.spines['bottom'].set_position('zero')
    ax.spines['left'].set_position('zero')

    # Remove top, right spines
    ax.spines['top'].set_visible(False)
    ax.spines['right'].set_visible(False)

    # Set x,y label on axes
    ax.set_xlabel('x', size=14, labelpad=-24, x=1.03)
    ax.set_ylabel('y', size=14, labelpad=-24, y=1.03, rotation=0)

    x_ticks = np.arange(xmin, xmax+tick_freq, tick_freq)
    y_ticks = np.arange(ymin, ymax+tick_freq, tick_freq)

    # Draw major and minor grid lines
    ax.grid(which='both', color='grey', linewidth=1, linestyle='-', alpha=0.2)

    ax.set_xticks(x_ticks[x_ticks != 0])
    ax.set_yticks(y_ticks[y_ticks != 0])

    # Arrows for axes
    arrow_fmt = dict(markersize=4, color='black', clip_on=False)
    ax.plot(1, 0, marker='>', transform=ax.get_yaxis_transform(),**arrow_fmt)
    ax.plot(0, 1, marker='^', transform=ax.get_xaxis_transform(),**arrow_fmt)

class DerivativeVisualization:
  def draw_f(ax, f, func_name, x_lim, y_lim, delta=0.01, X_in=None, alpha=1, tick_freq=1):
    X = X_in if (X_in is not None) else tf.range(x_lim[0] - delta, x_lim[1] + delta, delta=delta)

    X = tf.boolean_mask(X, tf.less(f(X), y_lim[1] + tick_freq))
    Y = f(X)

    # Draw f(x)
    ax.plot(X, Y, '-', alpha=alpha)
    ax.text(X[-1] + 0.5, Y[-1] - 0.5, func_name, fontsize=15)


from matplotlib import ticker

tf.random.set_seed(32)

x_domain = (-3, 3)
y_domain = (-3, 3)
fig, ax = plt.subplots(1, 2,figsize=(20,20))

### f(x)
f = lambda x: (np.e ** x)

ax[0].set_title('f(x)', pad=40, size=15)
CartesCoordinator.draw_coord(ax[0], x_domain, y_domain, aspect=1)
DerivativeVisualization.draw_f(ax[0], f, 'y = e^x', x_domain, y_domain)

### f'(x)
f = lambda x: (np.e**x)

ax[1].set_title('f\'(x)', pad=40, size=15)
CartesCoordinator.draw_coord(ax[1], x_domain, y_domain, aspect=1)
DerivativeVisualization.draw_f(ax[1], f, 'y = e^x', x_domain, y_domain)

plt.show()

import numpy as np
from IPython.display import HTML, Image
from matplotlib import animation, rc

rc('animation', html='html5')

tf.random.set_seed(32)

x_domain = (-3, 3)
y_domain = (-3, 3)
fig, ax = plt.subplots(1, 2, figsize=(20,10))

### f(x)
f = lambda x: (np.e ** x)

ax[0].set_title('f(x)', pad=40, size=15)
CartesCoordinator.draw_coord(ax[0], x_domain, y_domain, aspect=1)
DerivativeVisualization.draw_f(ax[0], f, 'y = e^x', x_domain, y_domain)

### f'(x)
f_prime = lambda x: (np.e**x)

ax[1].set_title('f\'(x)', pad=40, size=15)
CartesCoordinator.draw_coord(ax[1], x_domain, y_domain, aspect=1)
DerivativeVisualization.draw_f(ax[1], f_prime, 'y = e^x', x_domain, y_domain)

class AnimatedDerivative(object):
  """An animated changes in a function and its derivative function"""

  def __init__(self, fig, ax, f, f_prime, numpoints=50):
    self.scat = []
    self.texts = []

    self.f = f
    self.f_prime = f_prime

    self.fig, self.ax = fig, ax
    self.ani = animation.FuncAnimation(self.fig,
                                       self.animate,
                                       interval=500,
                                       init_func=self.setup_plot,
                                       frames=45,
                                       blit=True)
  
  def compute_slope(x, f):
    eps = 0.0001
    return (f(x+eps)-f(x))/eps

  def draw_tangent(x, f):
    k = AnimatedDerivative.compute_slope(x, f)
    X = np.linspace(-3, 3, 1000)
    Y = k*X + (f(x) - k*x)

    return X, Y

  def setup_plot(self):
    """Initial drawing"""
    self.texts.append(self.ax[0].text(-3, 2, f'',fontsize=20))
    self.texts.append(self.ax[1].text(-3, 2, f'',fontsize=20))

    self.scat.append(self.ax[0].scatter([], [], color='red', linewidths=20))
    self.scat.append(self.ax[1].scatter([], [], color='red', linewidths=20))

    self.tang, = self.ax[0].plot([], [], alpha=0.5, color='green', linewidth=3)
    self.m_tang = ax[0].text(-3, self.f(-3) - 1, '', fontsize=15, color='green')

    return self.texts + self.scat + [self.tang, self.m_tang]

  def animate(self, i):
    x = -3 + 0.1*i
    k = AnimatedDerivative.compute_slope(x, f)

    self.texts[0].set_text(f'x = {x: 4.2f}\ny = {self.f(x): 4.2f}')
    self.texts[1].set_text(f'x = {x: 4.2f}\ny = {self.f_prime(x): 4.2f}')
    
    self.scat[0].set_offsets([x, f(x)])
    self.scat[1].set_offsets([x, f_prime(x)])

    X, Y = AnimatedDerivative.draw_tangent(x, self.f)
    self.tang.set_data(X, Y)
    self.m_tang.set_text(f'm_tang = {k: 4.2f}')
    self.m_tang.set_position((x, f(x)-1))

    return self.texts + self.scat + [self.tang, self.m_tang]

plt.close()
a = AnimatedDerivative(fig, ax, f, f_prime)
a.ani.save('/content/drive/MyDrive/ML/calculus/sample.gif', writer='pillow')

Image(open('/content/drive/MyDrive/ML/calculus/sample.gif', 'rb').read())

trig_functions

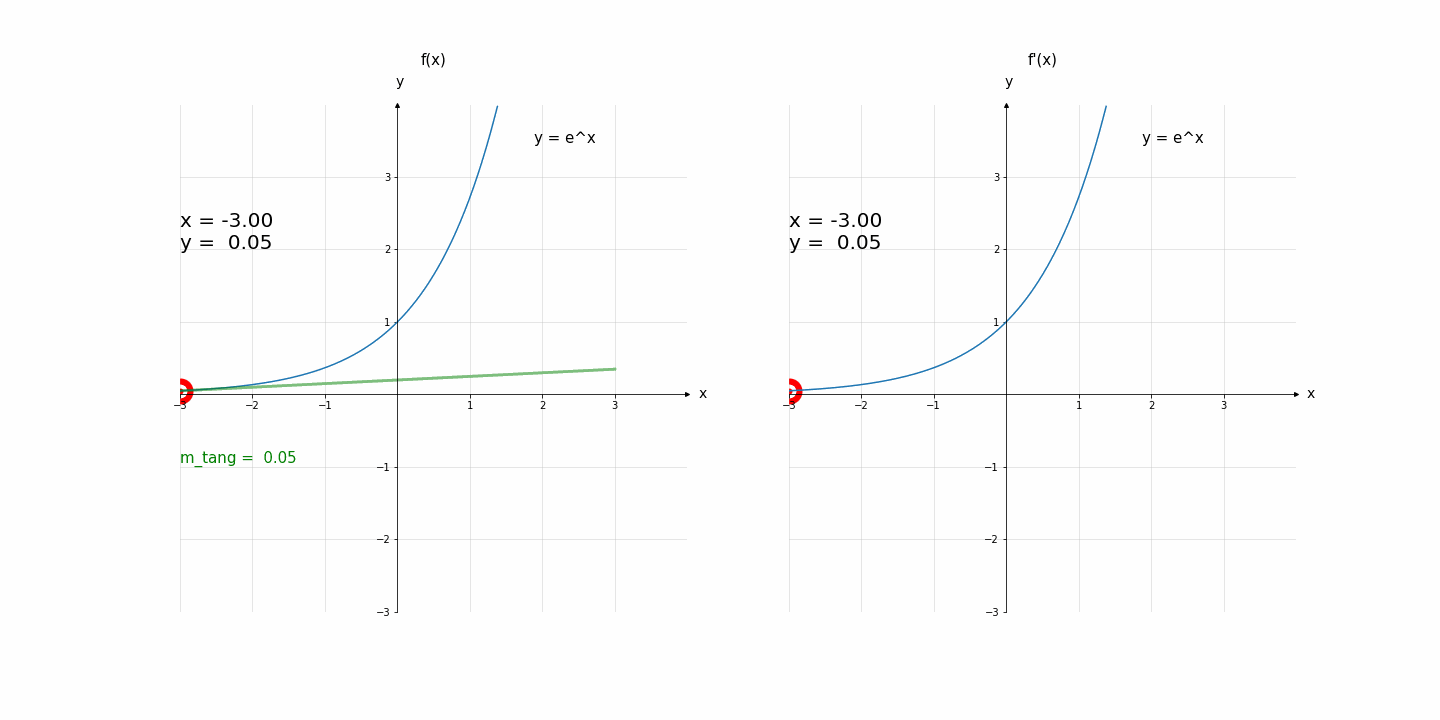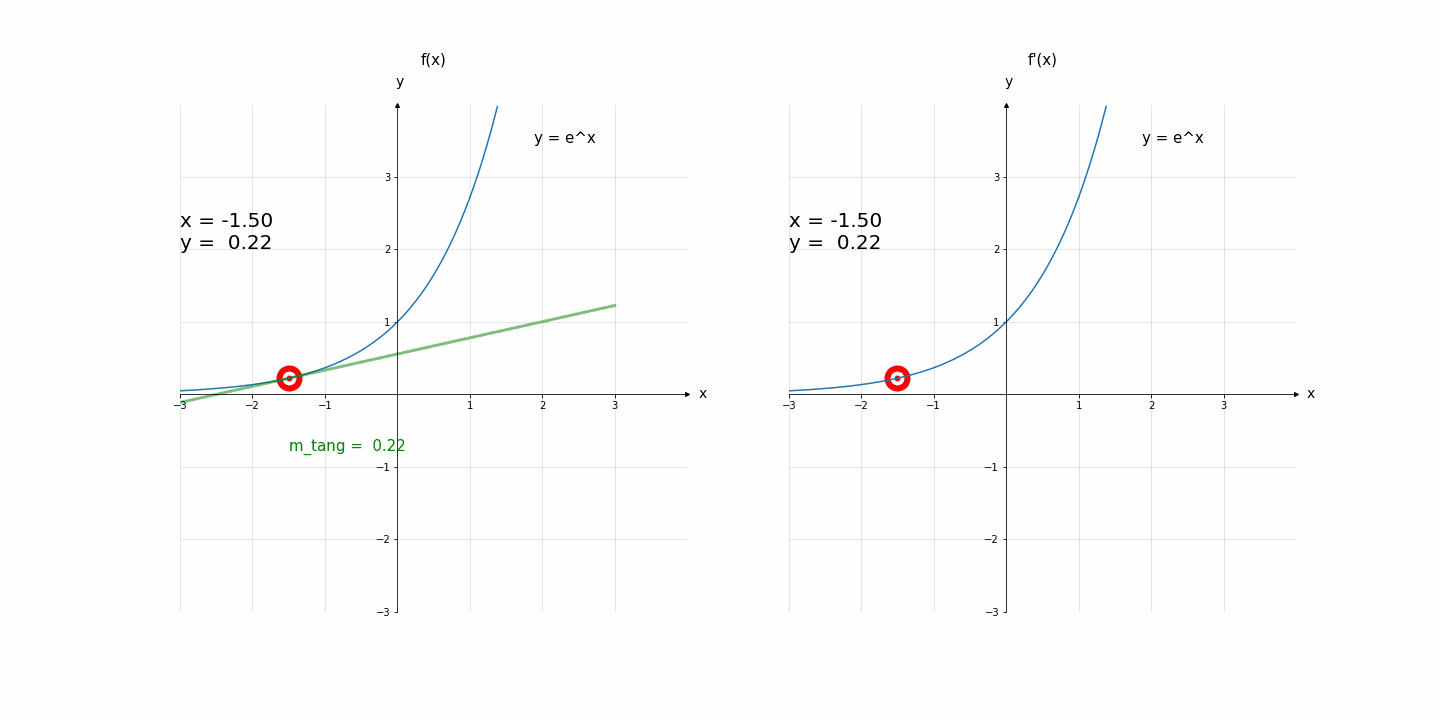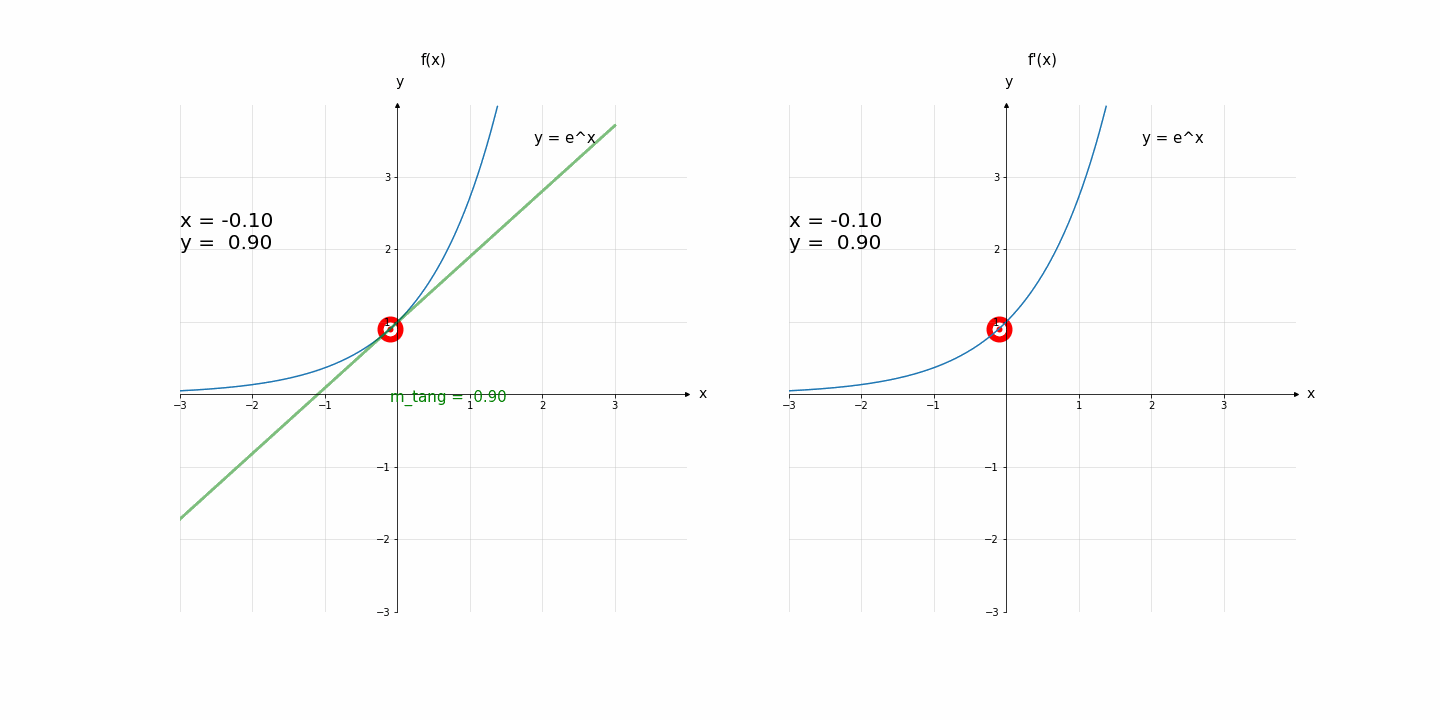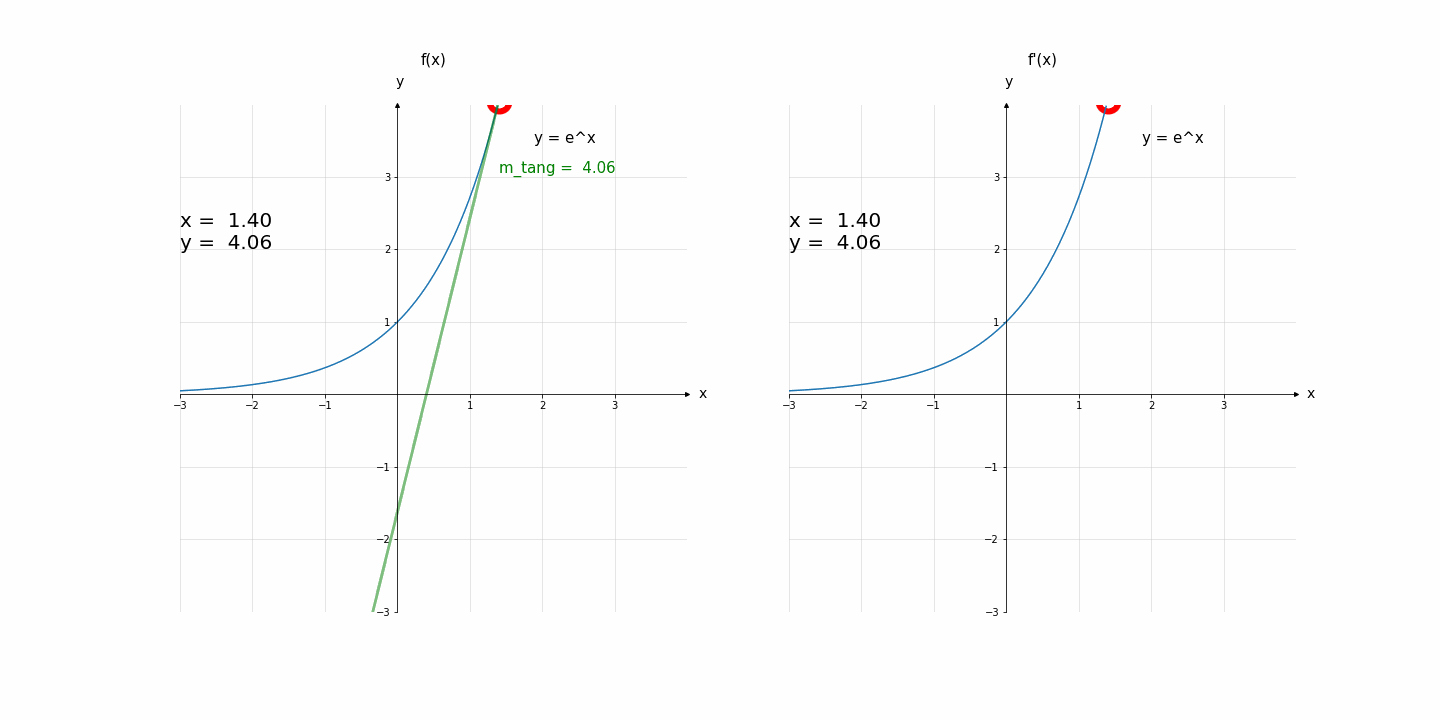
Code for Fig. 2 
import warnings
warnings.filterwarnings('ignore')
import logging
logging.basicConfig(
    format='%(asctime)s %(levelname)-8s %(message)s',
    level=logging.INFO,
    datefmt='%Y-%m-%d %H:%M:%S')

import tensorflow as tf
from matplotlib import pyplot as plt

import numpy as np

class CartesCoordinator:
  """
    Collection of utils for vector operation samples and exercise
  """
  def draw_coord(ax, xlim=(-5,5), ylim=(-5,5), tick_freq=1, aspect=1):
    xmin, xmax = xlim
    ymin, ymax = ylim

    ax.set(xlim=(xmin, xmax + tick_freq), ylim=(ymin, ymax + tick_freq), aspect=aspect)

    # Employ bottom, left spines as x,y axes
    ax.spines['bottom'].set_position('zero')
    ax.spines['left'].set_position('zero')

    # Remove top, right spines
    ax.spines['top'].set_visible(False)
    ax.spines['right'].set_visible(False)

    # Set x,y label on axes
    ax.set_xlabel('x', size=14, labelpad=-24, x=1.03)
    ax.set_ylabel('y', size=14, labelpad=-24, y=1.03, rotation=0)

    x_ticks = np.arange(xmin, xmax+tick_freq, tick_freq)
    y_ticks = np.arange(ymin, ymax+tick_freq, tick_freq)

    # Draw major and minor grid lines
    ax.grid(which='both', color='grey', linewidth=1, linestyle='-', alpha=0.2)

    ax.set_xticks(x_ticks[x_ticks != 0])
    ax.set_yticks(y_ticks[y_ticks != 0])

    # Arrows for axes
    arrow_fmt = dict(markersize=4, color='black', clip_on=False)
    ax.plot(1, 0, marker='>', transform=ax.get_yaxis_transform(),**arrow_fmt)
    ax.plot(0, 1, marker='^', transform=ax.get_xaxis_transform(),**arrow_fmt)

class DerivativeVisualization:
  def draw_f(ax, f, func_name, x_lim, y_lim, delta=0.01, X_in=None, alpha=1, tick_freq=1):
    X = X_in if (X_in is not None) else tf.range(x_lim[0] - delta, x_lim[1] + delta, delta=delta)

    X = tf.boolean_mask(X, tf.less(f(X), y_lim[1] + tick_freq))
    Y = f(X)

    # Draw f(x)
    ax.plot(X, Y, '-', alpha=alpha)
    ax.text(X[-1] + 0.5, Y[-1] - 0.5, func_name, fontsize=15)


from matplotlib import ticker

tf.random.set_seed(32)

x_domain = (-3, 3)
y_domain = (-3, 3)
fig, ax = plt.subplots(1, 2,figsize=(20,20))

### f(x)
f = lambda x: (np.e ** x)

ax[0].set_title('f(x)', pad=40, size=15)
CartesCoordinator.draw_coord(ax[0], x_domain, y_domain, aspect=1)
DerivativeVisualization.draw_f(ax[0], f, 'y = e^x', x_domain, y_domain)

### f'(x)
f = lambda x: (np.e**x)

ax[1].set_title('f\'(x)', pad=40, size=15)
CartesCoordinator.draw_coord(ax[1], x_domain, y_domain, aspect=1)
DerivativeVisualization.draw_f(ax[1], f, 'y = e^x', x_domain, y_domain)

plt.show()

import numpy as np
from IPython.display import HTML, Image
from matplotlib import animation, rc

rc('animation', html='html5')

tf.random.set_seed(32)

x_domain = (-3, 3)
y_domain = (-3, 3)
fig, ax = plt.subplots(1, 2, figsize=(20,10))

### f(x)
f = lambda x: (np.e ** x)

ax[0].set_title('f(x)', pad=40, size=15)
CartesCoordinator.draw_coord(ax[0], x_domain, y_domain, aspect=1)
DerivativeVisualization.draw_f(ax[0], f, 'y = e^x', x_domain, y_domain)

### f'(x)
f_prime = lambda x: (np.e**x)

ax[1].set_title('f\'(x)', pad=40, size=15)
CartesCoordinator.draw_coord(ax[1], x_domain, y_domain, aspect=1)
DerivativeVisualization.draw_f(ax[1], f_prime, 'y = e^x', x_domain, y_domain)

class AnimatedDerivative(object):
  """An animated changes in a function and its derivative function"""

  def __init__(self, fig, ax, f, f_prime, numpoints=50):
    self.scat = []
    self.texts = []

    self.f = f
    self.f_prime = f_prime

    self.fig, self.ax = fig, ax
    self.ani = animation.FuncAnimation(self.fig,
                                       self.animate,
                                       interval=500,
                                       init_func=self.setup_plot,
                                       frames=45,
                                       blit=True)
  
  def compute_slope(x, f):
    eps = 0.0001
    return (f(x+eps)-f(x))/eps

  def draw_tangent(x, f):
    k = AnimatedDerivative.compute_slope(x, f)
    X = np.linspace(-3, 3, 1000)
    Y = k*X + (f(x) - k*x)

    return X, Y

  def setup_plot(self):
    """Initial drawing"""
    self.texts.append(self.ax[0].text(-3, 2, f'',fontsize=20))
    self.texts.append(self.ax[1].text(-3, 2, f'',fontsize=20))

    self.scat.append(self.ax[0].scatter([], [], color='red', linewidths=20))
    self.scat.append(self.ax[1].scatter([], [], color='red', linewidths=20))

    self.tang, = self.ax[0].plot([], [], alpha=0.5, color='green', linewidth=3)
    self.m_tang = ax[0].text(-3, self.f(-3) - 1, '', fontsize=15, color='green')

    return self.texts + self.scat + [self.tang, self.m_tang]

  def animate(self, i):
    x = -3 + 0.1*i
    k = AnimatedDerivative.compute_slope(x, f)

    self.texts[0].set_text(f'x = {x: 4.2f}\ny = {self.f(x): 4.2f}')
    self.texts[1].set_text(f'x = {x: 4.2f}\ny = {self.f_prime(x): 4.2f}')
    
    self.scat[0].set_offsets([x, f(x)])
    self.scat[1].set_offsets([x, f_prime(x)])

    X, Y = AnimatedDerivative.draw_tangent(x, self.f)
    self.tang.set_data(X, Y)
    self.m_tang.set_text(f'm_tang = {k: 4.2f}')
    self.m_tang.set_position((x, f(x)-1))

    return self.texts + self.scat + [self.tang, self.m_tang]

plt.close()
a = AnimatedDerivative(fig, ax, f, f_prime)
a.ani.save('/content/drive/MyDrive/ML/calculus/sample.gif', writer='pillow')

Image(open('/content/drive/MyDrive/ML/calculus/sample.gif', 'rb').read())

ddx(ex)=exddx(ax)=axln⁡addx(ln⁡x)=1xddx(log⁡ax)=1xln⁡a \begin{aligned} &\frac{d}{dx}(e^x)=e^x & &\quad & &\frac{d}{dx}(a^x)=a^x \ln{a}\\ &\frac{d}{dx}(\ln{x}) = \frac{1}{x} & &\quad & &\frac{d}{dx}(\log_a{x})=\frac{1}{x\ln{a}} \end{aligned}

Inverse of Trig functions

Inverse Sine

y=sin⁡−1xdydx=11−x2 \begin{aligned} y &= \sin^{-1}{x}\\ \frac{dy}{dx} &= \frac{1}{\sqrt{1-x^2}} \end{aligned}

View proof

Inverse of Sine Proof

Suppose that y=sin⁡−1xy=\sin^{-1}{x}

We have:

f(f−1(x))=x  ⟹  f′(f−1(x))(f−1(x))′=1  ⟹  (f−1(x))′=1f′(f−1(x)) \begin{aligned} && f(f^-1(x)) &= x\\ &\implies & f^\prime\left(f^{-1}(x)\right)\left(f^{-1}(x)\right)^\prime &= 1\\ &\implies & \left(f^{-1}(x)\right)^\prime &= \frac{1}{f^\prime\left(f^{-1}(x)\right)} \end{aligned}

Let f(x)=sin⁡xf(x)=\sin{x} then:

(sin⁡−1x)′=1cos⁡(sin⁡−1x)(∗) \left(\sin^{-1}{x}\right)^\prime = \frac{1}{\cos\left(\sin^{-1}{x}\right)}\quad (*)

Secondly, we also have

y=sin⁡−1(x)  ⟹  sin⁡y=x,−π2≤y≤π2  ⟹  cos⁡y=1−x2  ⟺  cos⁡(sin⁡−1(x))=1−x2(∗∗) \begin{aligned} y = \sin^{-1}(x) &\implies \sin{y} &&= x , \quad \frac{-\pi}{2} \leq y \leq \frac{\pi}{2}\\ &\implies \cos{y} &&= \sqrt{1-x^2}\\ &\iff \cos{\left(\sin^{-1}(x)\right)} &&= \sqrt{1-x^2}\quad (**) \end{aligned}

From (∗),(∗∗)(*),(**) we could conclude that:

(sin⁡−1x)′=11−x2 \left(\sin^{-1}{x}\right)^\prime = \frac{1}{\sqrt{1-x^2}}

Summary: Inverse trig functions

ddx(sin⁡−1x)=11−x2ddx(cos⁡1x)=−11−x2ddx(tan⁡−1x)=11+x2ddx(cot⁡−1x)=−11+x2ddx(sec⁡−1x)=1∣x∣x2−1ddx(csc⁡−1x)=−1∣x∣x2−1 \begin{aligned} \frac{d}{dx}\left(\sin^{-1}{x}\right) &= \frac{1}{\sqrt{1-x^2}} & \frac{d}{dx}\left(\cos^{1}{x}\right) &= -\frac{1}{\sqrt{1-x^2}}\\ \frac{d}{dx}\left(\tan^{-1}{x}\right) &= \frac{1}{1+x^2} & \frac{d}{dx}\left(\cot^{-1}{x}\right) &= -\frac{1}{1+x^2}\\ \frac{d}{dx}\left(\sec^{-1}{x}\right) &= \frac{1}{\lvert x\rvert \sqrt{x^2-1}} & \frac{d}{dx}\left(\csc^{-1}{x}\right) &= -\frac{1}{\lvert x\rvert\sqrt{x^2-1}} \end{aligned}

References

  1. Wikipedia: Trigonometric functions. (2021). https://en.wikipedia.org/wiki/Trigonometric_functions
    [Online; accessed 2021-07-28]