Table of contents Preprequisites Exponentiation operation Power function Euler’s number e e e Exponential and Logarithmic functions Concept and Properties References Exponential and Logarithmic Functions
Exponentiation , involving two components: the base (b b b power (n n n b n = b × ⋯ × b ⏟ n times b^n = \underbrace{b\times \dots \times b}_{n\ \text{times}} b n = n times b × ⋯ × b
Properties of the exponentiation consists of:
a p + q = a p ⋅ a q a^{p+q} = a^p \cdot a^q a p + q = a p ⋅ a q ( a ⋅ b ) q = a q ⋅ b q (a\cdot b)^q = a^q \cdot b^q ( a ⋅ b ) q = a q ⋅ b q ( a b ) q = a q b q \left(\frac{a}{b}\right)^q = \frac{a^q}{b^q} ( b a ) q = b q a q ( a p ) q = a p q \left(a^p\right)^q = a^{pq} ( a p ) q = a p q Suppose n ∈ Q n \isin \mathbb{Q} n ∈ Q n ∈ R n \isin \mathbb{R} n ∈ R
f ( x ) = c x n f(x) = cx^n f ( x ) = c x n
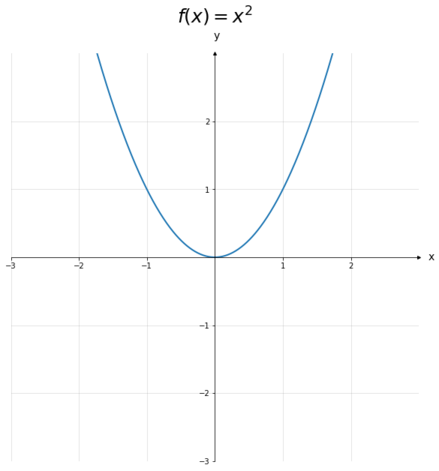
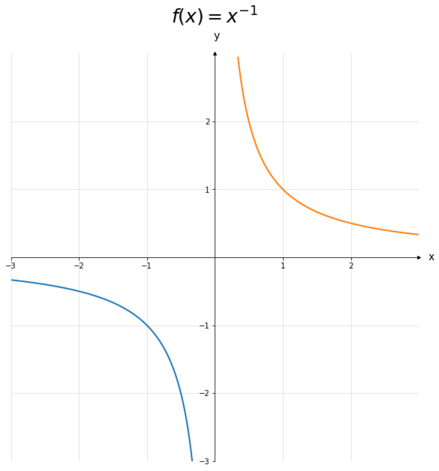
Relation Name Shape x ↦ x x\mapsto x x ↦ x Identity, Linear x ↦ x 2 x\mapsto x^2 x ↦ x 2 Quadratic x ↦ x 1 2 x\mapsto x^{\frac{1}{2}} x ↦ x 2 1 Square root x ↦ x − 1 x\mapsto x^{-1} x ↦ x − 1 Reciprocal
e e e By concept, the number e e e Euler’s number , is a mathematical constant which is an irrational number of
e = 2.71828182845904523536028747135266249775724709369995 … e = 2.71828182845904523536028747135266249775724709369995\dots e = 2 . 7 1 8 2 8 1 8 2 8 4 5 9 0 4 5 2 3 5 3 6 0 2 8 7 4 7 1 3 5 2 6 6 2 4 9 7 7 5 7 2 4 7 0 9 3 6 9 9 9 5 …
There are multiple approaches existed to explain the origin of this “unique” constant (just like how π \pi π
e e e base rate of exponential growth (Azad, 2021) The higher boundary for Area under the curve of 1 x \frac{1}{x} x 1 equal 1 . Suppose there is an exponential function
f ( x ) = a x , x ∈ R f(x) = a^x, x\isin \mathbb{R} f ( x ) = a x , x ∈ R
The first look into this function’s instant rate of change is:
d f d x = lim Δ x → 0 a x + Δ x − a x Δ x = a x ( lim t → 0 a t − 1 t ) = a x ( f ′ ( 0 ) ) ( 1 ) \begin{aligned} \frac{df}{dx} &= \lim_{\Delta{x}\to 0}{\frac{a^{x+\Delta{x}}-a^x}{\Delta{x}}}\\ &= a^x\left(\lim_{t\to 0}{\frac{a^t-1}{t}}\right)\\ &= a^x\left(f^\prime(0)\right) & (1) \end{aligned} d x d f = Δ x → 0 lim Δ x a x + Δ x − a x = a x ( t → 0 lim t a t − 1 ) = a x ( f ′ ( 0 ) ) ( 1 )
By observation, the instant change ratio of f ( x ) f(x) f ( x ) x = x 0 x=x_0 x = x 0 f ( x 0 ) f(x_0) f ( x 0 ) a constant of lim t → 0 a t − 1 t \lim_{t\to 0}{\frac{a^t-1}{t}} lim t → 0 t a t − 1 f ′ ( 0 ) f^\prime(0) f ′ ( 0 )
Base (a a a lim t → 0 a t − 1 t \lim_{t\to 0}{\frac{a^t-1}{t}} lim t → 0 t a t − 1 2 0.69314720407 3 1.09861234998 4 1.38629445701 6 1.79176007364 e e e 1
Due to the unique property of e e e lim t → 0 e t − 1 t = d d x ( e x ) ∣ x = 0 = e 0 = 1 ( 2 ) \begin{aligned} \lim_{t\to 0}{\frac{e^t-1}{t}} &= \frac{d}{dx}\left(e^x\right)\big|_{x=0}\\ &= e^0 \\ &= 1 && (2) \end{aligned} t → 0 lim t e t − 1 = d x d ( e x ) ∣ ∣ ∣ x = 0 = e 0 = 1 ( 2 )
This fact could be proved in a non-circular manner .
The property also makes the computation of derivative of f ( x ) = a x f(x) = a^x f ( x ) = a x a t a^t a t e t ln a e^{t\ln{a}} e t l n a h = t ln a h = t\ln{a} h = t ln a
lim t → 0 a t − 1 t = ln a ⋅ lim t ln a → 0 ( e t ln a − 1 t ln a ) = ln a ⋅ lim h → 0 ( e h − 1 h ) ⏟ Result = 1 = ln a ( 3 ) \begin{aligned} \lim_{t\to 0}{\frac{a^t-1}{t}} &= \ln{a}\cdot \lim_{t\ln{a}\to 0}{\left(\frac{e^{t\ln{a}}-1}{t\ln{a}}\right)}\\ &= \ln{a}\cdot \underbrace{\lim_{h\to 0}{\left(\frac{e^h-1}{h}\right)}}_{\text{Result =}1}\\[1.5em] &= \ln{a} & (3) \end{aligned} t → 0 lim t a t − 1 = ln a ⋅ t l n a → 0 lim ( t ln a e t l n a − 1 ) = ln a ⋅ Result = 1 h → 0 lim ( h e h − 1 ) = ln a ( 3 )
Thanks to e e e ( 2 ) (2) ( 2 ) ( 1 ) (1) ( 1 ) a ∈ R a\isin\mathbb{R} a ∈ R b b b e e e
a = exp ( ln a ) a = \exp{(\ln{a})} a = exp ( ln a )
The second picture on exponential growth: Compound Growth
Suppose the intial value is V V V R R R
Period Value Before Value After 1 V V V V + V R = V ( 1 + R ) V+VR = V(1+R) V + V R = V ( 1 + R ) 2 V ( 1 + R ) V(1+R) V ( 1 + R ) V ( 1 + R ) + R ⋅ V ( 1 + R ) = V ( 1 + R ) 2 V(1+R) + R\cdot V(1+R) = V(1+R)^2 V ( 1 + R ) + R ⋅ V ( 1 + R ) = V ( 1 + R ) 2 … n V ( 1 + R ) n − 1 V(1+R)^{n-1} V ( 1 + R ) n − 1 V ( 1 + R ) n V(1+R)^n V ( 1 + R ) n
Every period, the growth amount will grows at the same rate to contribute to the initial value, hence the term Compound growth .
V n = V 0 ⋅ ( 1 + R ) n ( 1 ) or V n = V 0 ⋅ ( 1 + rate ) period \begin{aligned} && V_n &= V_0\cdot (1+R)^n & (1)\\ &\text{or} & V_n &= V_0\cdot (1 + \text{rate})^{\text{period}} \end{aligned} or V n V n = V 0 ⋅ ( 1 + R ) n = V 0 ⋅ ( 1 + rate ) period ( 1 )
In the right side of the equation ( 1 ) (1) ( 1 ) R = 1 n R = \frac{1}{n} R = n 1 V 0 = 1 V_0 = 1 V 0 = 1
f ( n ) = ( 1 + 1 n ) n f(n) = \left(1+\frac{1}{n}\right)^n f ( n ) = ( 1 + n 1 ) n
\rule{20em}{0.3pt}
Investigating the behavior of f ( n ) f(n) f ( n )
The higher n n n f ( n ) f(n) f ( n ) f ( n ) f(n) f ( n ) n n n \rule{20em}{0.3pt}
Point #2 and the value of the limit mentioned a fact of:
lim n → ∞ ( 1 + 1 n ) n = c c is a constant \lim_{n\to \infty}{\left(1+\frac{1}{n}\right)^n} = c \quad\quad c \text{ is a constant} n → ∞ lim ( 1 + n 1 ) n = c c is a constant
Hint : c = e c = e c = e
Solution :
ln [ lim n → ∞ ( 1 + 1 n ) n ] = n ⋅ lim n → ∞ [ ln ( 1 + 1 n ) ] = lim 1 n → 0 [ ln ( 1 + 1 n ) 1 n ] ⏟ Result = 1 ⟺ lim n → ∞ ( 1 + 1 n ) n = e \begin{aligned} &&\ln{\left[\lim_{n\to\infty}{\left(1 + \frac{1}{n}\right)^n}\right]} &= n\cdot\lim_{n\to\infty}{\left[\ln{\left(1+\frac{1}{n}\right)}\right]}\\ &&&=\underbrace{\lim_{\frac{1}{n}\to 0}{\left[\frac{\ln{\left(1 + \frac{1}{n}\right)}}{\frac{1}{n}}\right]}}_{\text{Result = }\ 1}\\ &\iff & \lim_{n\to \infty}{\left(1+\frac{1}{n}\right)^n} = e \end{aligned} ⟺ ln [ n → ∞ lim ( 1 + n 1 ) n ] n → ∞ lim ( 1 + n 1 ) n = e = n ⋅ n → ∞ lim [ ln ( 1 + n 1 ) ] = Result = 1 n 1 → 0 lim [ n 1 ln ( 1 + n 1 ) ]
The concept could be generalized further into:
lim n → ∞ ( 1 + r n ) n = e r \lim_{n\to\infty}{\left(1 + \frac{r}{n}\right)^n} = e^r n → ∞ lim ( 1 + n r ) n = e r
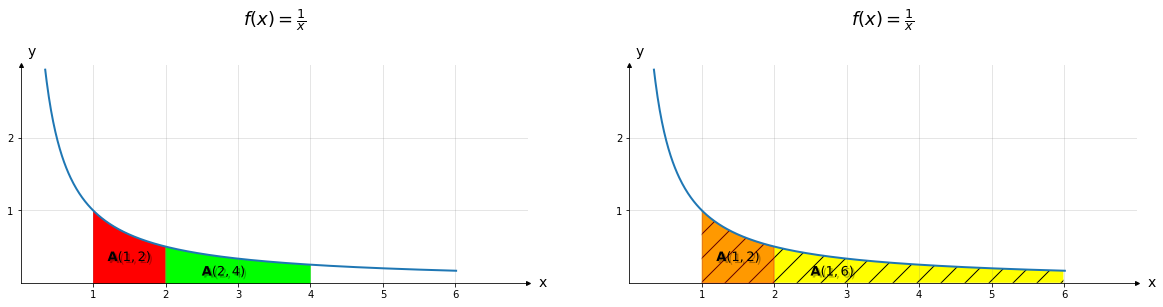
y = 1 x y = \frac{1}{x} y = x 1
Figure 1: Area under the curve of 1 x \frac{1}{x} x 1 (Singh, 2021)
The second popular characterization of e e e y = 1 / x y = 1/x y = 1 / x
To approximate the area under the curve of y = 1 / x y=1/x y = 1 / x x > 0 x > 0 x > 0 Δ x = 1 \Delta{x} = 1 Δ x = 1 1 / x 0 1/{x_0} 1 / x 0 A \mathbf{A} A 1 1 1
A = ∑ i = 1 ∞ A ( i , i + 1 ) ≈ ∑ i = 0 ∞ ( Δ x i ) ≈ ∑ i = 0 ∞ ( 1 i ) \begin{aligned} \mathbf{A} &= \sum_{i=1}^{\infty}{\mathbf{A}(i, i+1)}\\ &\approx \sum_{i=0}^{\infty}{\left(\frac{\Delta{x}}{i}\right)}\\ &\approx \sum_{i=0}^{\infty}{\left(\frac{1}{i}\right)} \end{aligned} A = i = 1 ∑ ∞ A ( i , i + 1 ) ≈ i = 0 ∑ ∞ ( i Δ x ) ≈ i = 0 ∑ ∞ ( i 1 )
The smaller the base is, the more accurate the area sum becomes:
A ( a , b ) = lim Δ x → 0 [ ∑ i = 0 a + i Δ x ≤ b ( Δ x a + i Δ x ) ] \mathbf{A}(a,b) = \lim_{\Delta{x}\to 0}{\left[\sum_{i=0}^{a+i\Delta{x} \leq b}{\left(\frac{\Delta{x}}{a+i\Delta{x}}\right)}\right]} A ( a , b ) = Δ x → 0 lim [ i = 0 ∑ a + i Δ x ≤ b ( a + i Δ x Δ x ) ]
Suppose we have a transformation ϕ : ( x , y ) ↦ ( 2 x , y / 2 ) \phi : (x, y) \mapsto (2x, y/2) ϕ : ( x , y ) ↦ ( 2 x , y / 2 ) ( 2 x 0 , 1 / 2 x 0 ) (2x_0, 1/{2x_0}) ( 2 x 0 , 1 / 2 x 0 ) y = 1 / x y=1/x y = 1 / x
A ( a , b ) = A ( 2 a , 2 b ) (Figure 1 - left) = A ( k a , k b ) k ∈ R \begin{aligned} \mathbf{A}(a,b) &= \mathbf{A}(2a,2b) & \text{(Figure 1 - left)}\\ &= \mathbf{A}(ka, kb) & k\isin\mathbb{R} \end{aligned} A ( a , b ) = A ( 2 a , 2 b ) = A ( k a , k b ) (Figure 1 - left) k ∈ R
In other words
A ( 1 , a b ) = A ( 1 , a ) + A ( a , a b ) = A ( 1 , a ) + A ( 1 , b ) \begin{aligned} \mathbf{A}(1,ab) &= \mathbf{A}(1, a) + \mathbf{A}{(a,ab)}\\ &= \mathbf{A}(1,a) + \mathbf{A}(1,b) \end{aligned} A ( 1 , a b ) = A ( 1 , a ) + A ( a , a b ) = A ( 1 , a ) + A ( 1 , b )
… which is similar to a property of logarithm functions:
ln a b = ln a + ln b \ln{ab} = \ln{a} + \ln{b} ln a b = ln a + ln b
WIP
Concept: exp : R ↦ R + ln : R + ↦ R Monotonicity: strictly increasing strictly increasing Continuity: continuous continuous Differentiability: differentiable differentiable Special cases: exp ( 1 ) = e exp ( 0 ) = 1 ln ( e ) = 1 ln ( 1 ) = 0 Arithmetics: exp ( x + y ) = exp x ⋅ exp y exp ( − x ) = 1 exp x ln ( x ⋅ y ) = ln x + ln y ln 1 x = − ln x Limit: lim x → 0 exp ( x ) − 1 x = 1 lim x → 0 ln ( 1 + x ) x = 1 Differentiation: d d x exp ( x ) = exp ( x ) d d x ln ( x ) = 1 x Function by limit: exp ( x ) = lim n → ∞ ( 1 + x n ) lim n → ∞ n ( x n − 1 ) Function by series: exp ( x ) = ∑ n = 0 ∞ x n n ! ∀ x ∈ R ln ( 1 + x ) = ∑ n = 1 ∞ ( − 1 ) n − 1 x n n ∀ x ∈ ( − 1 , 1 ] \begin{aligned} \footnotesize{\sf{\text{Concept:}}} &&\exp: \mathbb{R} \mapsto \mathbb{R}^+ &&\ &&\ln: \mathbb{R}^+\mapsto\mathbb{R}\quad\\ \footnotesize{\sf{\text{Monotonicity:}}} &&\text{strictly increasing} &&\ &&\text{strictly increasing}\quad\\ \footnotesize{\sf{\text{Continuity:}}} &&\text{continuous} &&\ &&\text{continuous}\quad\\ \footnotesize{\sf{\text{Differentiability:}}} &&\text{differentiable} &&\ &&\text{differentiable}\quad\\ \footnotesize{\sf{\text{Special cases:}}} &&\begin{aligned}\exp{(1)} = \boldsymbol{e}\\\exp{(0)}=1\end{aligned} &&\ &&\begin{aligned}\ln{(\boldsymbol{e})} = 1\\\ln{(1)}=0\end{aligned}\quad\\ \footnotesize{\sf{\text{Arithmetics:}}} &&\begin{aligned}\exp{(x+y)}=\exp{x}\cdot\exp{y}\\\exp{(-x)}=\frac{1}{\exp{x}}\end{aligned} &&\quad && \begin{aligned}\ln{(x\cdot y)}=\ln{x}+\ln{y}\\\ln{\frac{1}{x}}=-\ln{x}\end{aligned}\quad\\ \footnotesize{\sf{\text{Limit:}}} && \lim_{x\to 0}{\frac{\exp{(x)}-1}{x}}=1 &&\ && \lim_{x\to 0}{\frac{\ln{(1+x)}}{x}} = 1\quad\\ \footnotesize{\sf{\text{Differentiation:}}} && \frac{d}{dx}\exp{(x)} = \exp{(x)} &&\ && \frac{d}{dx}\ln{(x)} = \frac{1}{x}\quad\\ \footnotesize{\sf{\text{Function by limit:}}} && \exp{(x)} = \lim_{n\to\infty}{\left(1+\frac{x}{n}\right)} &&\ &&\lim_{n\to \infty}{n(\sqrt[n]{x}-1)}\quad\\ \footnotesize{\sf{\text{Function by series:}}} && \exp{(x)} = \sum_{n=0}^{\infty}{\frac{x^n}{n!}}\ \small{\forall x \isin \mathbb{R}} &&\ && \ln{(1+x)} = \sum_{n=1}^{\infty}{(-1)^{n-1}\frac{x^n}{n}}\ \small{\forall x\isin \left(-1,1\right]}\quad \end{aligned} Concept: Monotonicity: Continuity: Differentiability: Special cases: Arithmetics: Limit: Differentiation: Function by limit: Function by series: exp : R ↦ R + strictly increasing continuous differentiable exp ( 1 ) = e exp ( 0 ) = 1 exp ( x + y ) = exp x ⋅ exp y exp ( − x ) = exp x 1 x → 0 lim x exp ( x ) − 1 = 1 d x d exp ( x ) = exp ( x ) exp ( x ) = n → ∞ lim ( 1 + n x ) exp ( x ) = n = 0 ∑ ∞ n ! x n ∀ x ∈ R ln : R + ↦ R strictly increasing continuous differentiable ln ( e ) = 1 ln ( 1 ) = 0 ln ( x ⋅ y ) = ln x + ln y ln x 1 = − ln x x → 0 lim x ln ( 1 + x ) = 1 d x d ln ( x ) = x 1 n → ∞ lim n ( n x − 1 ) ln ( 1 + x ) = n = 1 ∑ ∞ ( − 1 ) n − 1 n x n ∀ x ∈ ( − 1 , 1 ]
To prove these elementary properties of the exponetial and logarithmic functions, one have to establish the aforementioned properties in a non-circular manner. (Singh, 2021)
There are three ways to accomplish the tasks:
Logarithmic function as an integral Exponetial function as a limit Azad, K. (2021). An Intuitive Guide To Exponential Functions & e . https://betterexplained.com/articles/an-intuitive-guide-to-exponential-functions-e[Online; accessed 2021-09-08]
Singh, P. (2021). Theories of Exponential and Logarithmic Functions . https://paramanands.blogspot.com/2014/05/theories-of-exponential-and-logarithmic-functions-part-1.html[Online; accessed 2021-09-05]